Munich Agreement
 From left to right: Neville Chamberlain, Édouard Daladier, Adolf Hitler, Benito Mussolini, and Galeazzo Ciano pictured before signing the Munich Agreement (1938) | |
| Signed | 30 September 1938 |
|---|---|
| Location | Munich, Germany |
| Signatories | |
| Parties | |
The Munich Agreement[a] was an agreement reached in Munich on 30 September 1938, by Nazi Germany, the United Kingdom, the French Republic, and Fascist Italy. The agreement provided for the German annexation of part of Czechoslovakia called the Sudetenland, where more than three million people, mainly ethnic Germans, lived.[1] The pact is also known in some areas as the Munich Betrayal (Czech: Mnichovská zrada; Slovak: Mníchovská zrada), because of a previous 1924 alliance agreement[2] and a 1925 military pact between France and the Czechoslovak Republic.
Germany had started a low-intensity undeclared war on Czechoslovakia on 17 September 1938. In reaction, Britain and France on 20 September formally requested Czechoslovakia cede the Sudetenland territory to Germany. This was followed by Polish and Hungarian territorial demands brought on 21 and 22 September, respectively. Meanwhile, German forces conquered parts of the Cheb District and Jeseník District, where local battles included use of German artillery, Czechoslovak tanks, and armored vehicles. Lightly armed German infantry briefly overran other border counties before being repelled. Poland also grouped its army units near its common border with Czechoslovakia and conducted an unsuccessful probing offensive on 23 September.[3] Hungary moved its troops towards the border with Czechoslovakia, without attacking. The Soviet Union announced its willingness to come to Czechoslovakia's assistance, provided that the Red Army would be able to cross Polish and Romanian territory. Both countries refused to allow the Soviet army to use their territories.[4]
An emergency meeting of the main European powers–not including Czechoslovakia, although their representatives were present in the town, or the Soviet Union, an ally to both France and Czechoslovakia–took place in Munich, Germany, on 29–30 September 1938. An agreement was quickly reached on Hitler's terms, and signed by the leaders of Germany, France, Britain, and Italy. The Czechoslovak mountainous borderland marked a natural border between the Czech state and the Germanic states since the early Middle Ages; it also presented a major natural obstacle to a possible German attack. Strengthened by significant border fortifications, the Sudetenland was of absolute strategic importance to Czechoslovakia.
On 30 September, Czechoslovakia submitted to the combination of military pressure by Germany, Poland, and Hungary, and diplomatic pressure by Britain and France, and agreed to surrender territory to Germany following the Munich terms.
The Munich Agreement was soon followed by the First Vienna Award on 2 November 1938, separating largely Hungarian inhabited territories in southern Slovakia and southern Subcarpathian Rus' from Czechoslovakia. On 30 November 1938, Czechoslovakia ceded to Poland small patches of land in the Spiš and Orava regions.[5]
In March 1939, the First Slovak Republic, a German puppet state, proclaimed its independence. Shortly afterwards, Hitler reneged on his promises to respect the integrity of Czechoslovakia by occupying the remainder of the country and creating the Protectorate of Bohemia and Moravia.[6] The conquered nation's significant military arsenal played an important role in Germany's invasions of Poland and France in 1939 and 1940.[7]
Much of Europe celebrated the Munich Agreement, as they considered it a way to prevent a major war on the continent.[8][9] Adolf Hitler announced that it was his last territorial claim in Northern Europe. Today, the Munich Agreement is widely regarded as a failed act of appeasement, and the term has become "a byword for the futility of appeasing expansionist totalitarian states."[10]
History
[edit]| Territorial evolution of Germany in the 20th century |
|---|
| Events leading to World War II |
|---|
Background
[edit]Demands for autonomy
[edit]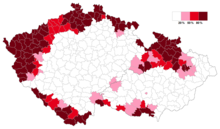


The First Czechoslovak Republic was created in 1918 after the collapse of the Austro-Hungarian Empire at the end of World War I. The Treaty of Saint-Germain recognized the independence of Czechoslovakia and the Treaty of Trianon defined the borders of the new state, which was divided in to the regions of Bohemia and Moravia in the west and Slovakia and Subcarpathian Rus' in the east, including more than three million Germans, 22.95% of the total population of the country. They lived mostly in border regions of the historical Czech Lands for which they coined the new name Sudetenland, which bordered on Germany and the newly created country of Austria.[12]
The Sudeten Germans were not consulted on whether they wished to be citizens of Czechoslovakia. Although the constitution guaranteed equality for all citizens, there was a tendency among political leaders to transform the country "into an instrument of Czech and Slovak nationalism."[13] Some progress was made to integrate the Germans and other minorities, but they continued to be underrepresented in the government and the army. Moreover, the Great Depression beginning in 1929 impacted the highly industrialized and export-oriented Sudeten Germans more than it did the Czech and Slovak populations. By 1936, 60 percent of the unemployed people in Czechoslovakia were Germans.[14]
In 1933, Sudeten German leader Konrad Henlein founded the Sudeten German Party (SdP), which was "militant, populist, and openly hostile" to the Czechoslovak government. It soon captured two-thirds of the vote in districts with a heavy German population. Historians differ as to whether the SdP was a Nazi front organisation from its beginning, or if it evolved into one.[15][16] By 1935, the SdP was the second-largest political party in Czechoslovakia as German votes concentrated on this party, and Czech and Slovak votes were spread among several parties.[15]
Shortly after the Anschluss of Austria to Germany, Henlein met with Hitler in Berlin on 28 March 1938, and was instructed to make demands unacceptable to the democratic Czechoslovak government, led by President Edvard Beneš. On 24 April, the SdP issued a series of demands known as the Karlsbader Programm. [17] Henlein demanded autonomy for Germans in Czechoslovakia.[15] The Czechoslovak government responded by saying that it was willing to provide more minority rights to the German minority but was initially reluctant to grant autonomy.[15] The SdP gained 88% of the ethnic German votes in May 1938.[18]
With tension high between the Germans and the Czechoslovak government, Beneš, on 15 September 1938, secretly offered to give 6,000 square kilometres (2,300 sq mi) of Czechoslovakia to Germany, in exchange for a German agreement to admit 1.5 to 2.0 million Sudeten Germans expelled by Czechoslovakia. Hitler did not reply.[19]
Sudeten crisis
[edit]As the previous appeasement of Hitler had shown, France and Britain were intent on avoiding war. The French government did not wish to face Germany alone and took its lead from British Conservative government of Prime Minister Neville Chamberlain. He considered the Sudeten German grievances justified and believed Hitler's intentions to be limited. Both Britain and France, therefore, advised Czechoslovakia to accede to Germany's demands. Beneš resisted and, on 19 May, initiated a partial mobilization in response to a possible German invasion.[20]
On 20 May, Hitler presented his generals with a draft plan of attack on Czechoslovakia that was codenamed Operation Green.[21] He insisted that he would not "smash Czechoslovakia" militarily without "provocation", "a particularly favourable opportunity" or "adequate political justification."[22] On 28 May, Hitler called a meeting of his service chiefs, ordered an acceleration of U-boat construction and brought forward the construction of his new battleships, Bismarck and Tirpitz, to spring 1940. He demanded that the increase in the firepower of the battleships Scharnhorst and Gneisenau be accelerated.[23] While recognizing that this would still be insufficient for a full-scale naval war with Britain, Hitler hoped it would be a sufficient deterrent.[24] Ten days later, Hitler signed a secret directive for war against Czechoslovakia to begin no later than 1 October.[23]
On 22 May, Juliusz Łukasiewicz, the Polish ambassador to France, told French Foreign Minister Georges Bonnet that if France moved against Germany to defend Czechoslovakia, "We shall not move." Łukasiewicz also told Bonnet that Poland would oppose any attempt by Soviet forces to defend Czechoslovakia from Germany. Édouard Daladier told Jakob Suritz, the Soviet ambassador to France, "Not only can we not count on Polish support but we have no faith that Poland will not strike us in the back."[25] However, the Polish government indicated multiple times (in March 1936 and May, June and August 1938) that it was prepared to fight Germany if the French decided to help Czechoslovakia: "Beck's proposal to Bonnet, his statements to Ambassador Drexel Biddle, and the statement noted by Vansittart, show that the Polish foreign minister was, indeed, prepared to carry out a radical change of policy if the Western powers decided on war with Germany. However, these proposals and statements did not elicit any reaction from British and French governments that were bent on averting war by appeasing Germany."[3]

Hitler's adjutant, Fritz Wiedemann, recalled after the war that he was "very shocked" by Hitler's new plans to attack Britain and France three to four years after "deal[ing] with the situation" in Czechoslovakia.[26] General Ludwig Beck, chief of the German general staff, noted that Hitler's change of heart in favour of quick action was because Czechoslovak defences were still being improvised, which would no longer be the case two to three years later, and British rearmament would not come into effect until 1941 or 1942.[24] General Alfred Jodl noted in his diary that the partial Czechoslovak mobilization of 21 May had led Hitler to issue a new order for Operation Green on 30 May and that it was accompanied by a covering letter from Wilhelm Keitel that stated that the plan must be implemented by 1 October at the very latest.[24]
In the meantime, the British government demanded that Beneš request a mediator. Not wishing to sever his government's ties with Western Europe, Beneš reluctantly accepted. The British appointed Lord Runciman, a former Liberal cabinet minister, who arrived in Prague on 3 August with instructions to persuade Beneš to agree to a plan acceptable to the Sudeten Germans.[27] On 20 July, Bonnet told the Czechoslovak ambassador in Paris that while France would declare its support in public to help the Czechoslovak negotiations, it was not prepared to go to war over Sudetenland.[27] In August, the German press was full of stories alleging Czechoslovak atrocities against Sudeten Germans, with the intention of forcing the West into putting pressure on the Czechoslovaks to make concessions.[28] Hitler hoped that the Czechoslovaks would refuse and that the West would then feel morally justified in leaving the Czechoslovaks to their fate.[29] In August, Germany sent 750,000 soldiers along the border of Czechoslovakia, officially as part of army maneuvres.[15][29] On 4 or 5 September,[27] Beneš submitted the Fourth Plan, granting nearly all the demands of the agreement. The Sudeten Germans were under instruction from Hitler to avoid a compromise,[29] and the SdP held demonstrations that provoked a police action in Ostrava on 7 September, in which two of their parliamentary deputies were arrested.[27] The Sudeten Germans used the incident and false allegations of other atrocities as an excuse to break off further negotiations.[27][30]

On 12 September, Hitler made a speech at a Nazi Party rally in Nuremberg on the Sudeten crisis condemning the actions of the government of Czechoslovakia.[15] Hitler denounced Czechoslovakia as being a fraudulent state that was in violation of international law's emphasis of national self-determination, claiming it was a Czech hegemony although the Germans, the Slovaks, the Hungarians, the Ukrainians and the Poles of the country actually wanted to be in a union with the Czechs.[31] Hitler accused Beneš of seeking to gradually exterminate the Sudeten Germans and claimed that since Czechoslovakia's creation, over 600,000 Germans had been intentionally forced out of their homes under the threat of starvation if they did not leave.[32] He alleged that Beneš's government was persecuting Germans along with Hungarians, Poles, and Slovaks and accused Beneš of threatening the nationalities with being branded traitors if they were not loyal to the country.[31] He stated that he, as the head of state of Germany, would support the right of the self-determination of fellow Germans in the Sudetenland.[31] He condemned Beneš for his government's recent execution of several German protesters.[31] He accused Beneš of being belligerent and threatening behaviour towards Germany which, if war broke out, would result in Beneš forcing Sudeten Germans to fight against their will against Germans from Germany.[31] Hitler accused the government of Czechoslovakia of being a client regime of France, claiming that the French Minister of Aviation Pierre Cot had said, "We need this state as a base from which to drop bombs with greater ease to destroy Germany's economy and its industry."[32]
Berchtesgaden meeting
[edit]
On 13 September, after internal violence and disruption in Czechoslovakia ensued, Chamberlain asked Hitler for a personal meeting to find a solution to avert a war.[33] Chamberlain decided to do this after conferring with his advisors Lord Halifax, Sir John Simon, and Sir Samuel Hoare. The meeting was announced at a special press briefing at 10 Downing Street, and led to a swell of optimism in British public opinion.[34] Chamberlain arrived by a chartered British Airways Lockheed Electra in Germany on 15 September and then arrived at Hitler's residence in Berchtesgaden for the meeting.[35] The flight was one of the first times a head of state or diplomatic official flew to a diplomatic meeting in an airplane, as the tense situation left little time to take a train or boat.[34] Henlein flew to Germany on the same day.[33] That day, Hitler and Chamberlain held discussions in which Hitler insisted that the Sudeten Germans must be allowed to exercise the right of national self-determination and be able to join Sudetenland with Germany. Hitler repeatedly falsely claimed that the Czechoslovak government had killed 300 Sudeten Germans.[34] Hitler also expressed concern to Chamberlain about what he perceived as British "threats."[35] Chamberlain responded that he had not issued "threats" and in frustration asked Hitler "Why did I come over here to waste my time?"[35] Hitler responded that if Chamberlain was willing to accept the self-determination of the Sudeten Germans, he would be willing to discuss the matter.[35] Hitler also convinced Chamberlain that he did not truly wish to destroy Czechoslovakia, but that he believed that upon a German annexation of the Sudetenland the country's minorities would each secede and cause the country to collapse.[34] Chamberlain and Hitler held discussions for three hours, and the meeting adjourned. Chamberlain flew back to Britain and met with his cabinet to discuss the issue.[35]
After the meeting, Daladier flew to London on 16 September to meet with British officials to discuss a course of action.[36] The situation in Czechoslovakia became tenser that day, with the Czechoslovak government issuing an arrest warrant for Henlein, who had arrived in Germany a day earlier to take part in the negotiations.[37] The French proposals ranged from waging war against Germany to supporting the Sudetenland being ceded to Germany.[37] The discussions ended with a firm British-French plan in place.[37] Britain and France demanded that Czechoslovakia cede to Germany all territories in which the German population represented over 50% of the Sudetenland's total population.[37] In exchange for that concession, Britain and France would guarantee the independence of Czechoslovakia.[37] Czechoslovakia rejected the proposed solution.[37]

On 17 September 1938 Hitler ordered the establishment of Sudetendeutsches Freikorps, a paramilitary organization that took over the structure of Ordnersgruppe, an organization of ethnic Germans in Czechoslovakia that had been dissolved by the Czechoslovak authorities the previous day due to its implication in a large number of terrorist activities. The organization was sheltered, trained and equipped by German authorities and conducted cross-border terrorist operations into Czechoslovak territory. Relying on the Convention for the Definition of Aggression, Czechoslovak president Edvard Beneš[38] and the government-in-exile[39] later regarded 17 September 1938 as the beginning of the undeclared German-Czechoslovak war. This understanding has been assumed also by the contemporary Czech Constitutional court.[40] In the following days, Czechoslovak forces suffered over 100 personnel killed in action, hundreds wounded and over 2,000 abducted to Germany.
On 18 September, Italy's Duce Benito Mussolini made a speech in Trieste, Italy, where he declared "If there are two camps, for and against Prague, let it be known that Italy has chosen its side", with the clear implication being that Mussolini supported Germany in the crisis.[35]
On 20 September, German opponents within the military met to discuss the final plans of a plot they had developed to overthrow the Nazi regime. The meeting was led by General Hans Oster, the deputy head of the Abwehr (Germany's counter-espionage agency). Other members included Captain Friedrich Wilhelm Heinz, and other military officers leading the planned coup d'etat met at the meeting.[41] On 22 September, Chamberlain, about to board his plane to go to Germany for further talks at Bad Godesberg, told the press who met him there that "My objective is peace in Europe, I trust this trip is the way to that peace."[37] Chamberlain arrived in Cologne, where he received a lavish grand welcome with a German band playing "God Save the King" and Germans giving Chamberlain flowers and gifts.[37] Chamberlain had calculated that fully accepting German annexation of all of the Sudetenland with no reductions would force Hitler to accept the agreement.[37] Upon being told of this, Hitler responded "Does this mean that the Allies have agreed with Prague's approval to the transfer of the Sudetenland to Germany?", Chamberlain responded "Precisely", to which Hitler responded by shaking his head, saying that the Allied offer was insufficient. He told Chamberlain that he wanted Czechoslovakia to be completely dissolved and its territories redistributed to Germany, Poland, and Hungary, and told Chamberlain to take it or leave it.[37] Chamberlain was shaken by this statement.[37] Hitler went on to tell Chamberlain that since their last meeting on the 15th, Czechoslovakia's actions, which Hitler claimed included killings of Germans, had made the situation unbearable for Germany.[37]
Later in the meeting, a deception was undertaken to influence and put pressure on Chamberlain: one of Hitler's aides entered the room to inform Hitler of more Germans being killed in Czechoslovakia, to which Hitler screamed in response "I will avenge every one of them. The Czechs must be destroyed."[37] The meeting ended with Hitler refusing to make any concessions to the Allies' demands.[37] Later that evening, Hitler grew worried that he had gone too far in pressuring Chamberlain, and telephoned Chamberlain's hotel suite, saying that he would accept annexing only the Sudetenland, with no designs on other territories, provided that Czechoslovakia begin the evacuation of ethnic Czechs from the German majority territories by 26 September at 8:00am. After being pressed by Chamberlain, Hitler agreed to have the ultimatum set for 1 October (the same date that Operation Green was set to begin).[42] Hitler then said to Chamberlain that this was one concession that he was willing to make to the Prime Minister as a "gift" out of respect for the fact that Chamberlain had been willing to back down somewhat on his earlier position.[42] Hitler went on to say that upon annexing the Sudetenland, Germany would hold no further territorial claims upon Czechoslovakia and would enter into a collective agreement to guarantee the borders of Germany and Czechoslovakia.[42]
A new Czechoslovak cabinet, under General Jan Syrový, was installed and on 23 September a decree of general mobilization was issued which was accepted by the public with a strong enthusiasm – within 24 hours, one million men joined the army to defend the country. The Czechoslovak Army, modern, experienced and possessing an excellent system of frontier fortifications, was prepared to fight. The Soviet Union announced its willingness to come to Czechoslovakia's assistance, provided that the Red Army would be able to cross Polish and Romanian territory. Both countries refused to allow the Soviet army to use their territories.[43]
In the early hours of 24 September, Hitler issued the Godesberg Memorandum, which demanded that Czechoslovakia cede the Sudetenland to Germany no later than 28 September, with plebiscites to be held in unspecified areas under the supervision of German and Czechoslovak forces. The memorandum also stated that if Czechoslovakia did not agree to the German demands by 2 pm on 28 September, Germany would take the Sudetenland by force. On the same day, Chamberlain returned to Britain and announced that Hitler demanded the annexation of the Sudetenland without delay.[42] The announcement enraged those in Britain and France who wanted to confront Hitler once and for all, even if it meant war, and its supporters gained strength.[42] The Czechoslovak Ambassador to the United Kingdom, Jan Masaryk, was elated upon hearing of the support for Czechoslovakia from British and French opponents of Hitler's plans, saying "The nation of Saint Wenceslas will never be a nation of slaves."[42]

On 25 September, Czechoslovakia agreed to the conditions previously agreed upon by Britain, France, and Germany. The next day, however, Hitler added new demands, insisting that the claims of ethnic Germans in Poland and Hungary also be satisfied.
On 26 September, Chamberlain sent Sir Horace Wilson to carry a personal letter to Hitler declaring that the Allies wanted a peaceful resolution to the Sudeten crisis.[42] Later that evening, Hitler made his response in a speech at the Berlin Sportpalast; he claimed that the Sudetenland was "the last territorial demand I have to make in Europe"[44] and gave Czechoslovakia a deadline of 28 September at 2:00 pm to cede the Sudetenland to Germany or face war.[42] At this point the British government began to make war preparations, and the House of Commons was reconvened from a parliamentary recess.[34]
On 27 September 1938, when negotiations between Hitler and Chamberlain were strained, Chamberlain addressed the British people, saying, in particular: "How horrible, fantastic, incredible it is that we should be digging trenches and trying on gas masks here because of a quarrel in a far-away country between people of whom we know nothing."[45]
On 28 September at 10:00 am, four hours before the deadline and with no agreement to Hitler's demand by Czechoslovakia, the British ambassador to Italy, Lord Perth, called Italy's Foreign Minister Galeazzo Ciano to request an urgent meeting.[42] Perth informed Ciano that Chamberlain had instructed him to request that Mussolini enter the negotiations and urge Hitler to delay the ultimatum.[42] At 11:00 am, Ciano met Mussolini and informed him of Chamberlain's proposition; Mussolini agreed with it and responded by telephoning Italy's ambassador to Germany and told him "Go to the Fuhrer at once, and tell him that whatever happens, I will be at his side, but that I request a twenty-four-hour delay before hostilities begin. In the meantime, I will study what can be done to solve the problem."[46] Hitler received Mussolini's message while in discussions with the French ambassador. Hitler responded "My good friend, Benito Mussolini, has asked me to delay for twenty-four hours the marching orders of the German army, and I agreed." Of course, this was no concession, as the invasion date was set for 1 October 1938.[47] Upon speaking with Chamberlain, Lord Perth gave Chamberlain's thanks to Mussolini as well as Chamberlain's request that Mussolini attend a four-power conference of Britain, France, Germany, and Italy in Munich on 29 September to settle the Sudeten problem prior to the deadline of 2:00 pm. Mussolini agreed.[47] Hitler's only request was to make sure that Mussolini be involved in the negotiations at the conference.[47] Nevile Henderson, Alexander Cadogan, and Chamberlain's personal secretary Lord Dunglass passed the news of the conference to Chamberlain while he was addressing Parliament, and Chamberlain suddenly announced the conference and his acceptance to attend at the end of the speech to cheers.[34] When United States President Franklin D. Roosevelt learned the conference had been scheduled, he telegraphed Chamberlain, "Good man."[48]
Resolution
[edit]
1. The Sudetenland became part of Germany in accordance with the Munich Agreement (October 1938).
2. Poland annexes Trans-Olza, an area with a Polish plurality, over which the two countries had fought a war in 1919 (October 1938).
3. Border areas (southern third of Slovakia and southern Carpathian Ruthenia) with Hungarian minorities became part of Hungary in accordance with the First Vienna Award (November 1938).
4. On 15 March 1939, during the German invasion of the remaining Czech territories, Hungary annexes the remainder of Carpathian Ruthenia (which had been autonomous since October 1938).
5. Germany establishes the Protectorate of Bohemia and Moravia with a puppet government, on 16 March 1939.
6. On 14 March 1939, a pro-Hitler Catholic-fascist government declares the Slovak Republic, as an Axis client state.

Discussions began at the Führerbau immediately after Chamberlain and Daladier arrived, giving them little time to consult. The meeting was held in English, French, and German.[34] A deal was reached on 29 September, and at about 1:30 a.m. on 30 September 1938,[49] Adolf Hitler, Neville Chamberlain, Benito Mussolini and Édouard Daladier signed the Munich Agreement. The agreement was officially introduced by Mussolini although in fact the Italian plan was nearly identical to the Godesberg proposal: the German army was to complete the occupation of the Sudetenland by 10 October, and an international commission would decide the future of other disputed areas.[50]
Czechoslovakia was informed by Britain and France that it could either resist Nazi Germany alone or submit to the prescribed annexations. The Czechoslovak government, realizing the hopelessness of fighting the Nazis alone, reluctantly capitulated (30 September) and agreed to abide by the agreement. The settlement gave Germany the Sudetenland starting 10 October, and de facto control over the rest of Czechoslovakia as long as Hitler promised to go no further. On 30 September after some rest, Chamberlain went to Hitler's apartment in the Prinzregentenstraße and asked him to sign a statement calling the Anglo-German Naval Agreement "symbolic of the desire of our two countries never to go to war with one another again." After Hitler's interpreter translated it for him, he happily agreed.[34]
On 30 September, upon his return to Britain, Chamberlain delivered his controversial "peace for our time" speech to crowds in London.[51]


Reactions
[edit]Immediate response
[edit]Czechoslovakia
[edit]The Czechoslovaks were dismayed with the Munich settlement. They were not invited to the conference and felt they had been betrayed by the British and French governments. Many Czechs and Slovaks refer to the Munich Agreement as the Munich Diktat (Czech: Mnichovský diktát; Slovak: Mníchovský diktát). The phrase "Munich Betrayal" (Mnichovská zrada; Mníchovská zrada) is also used because the military alliance Czechoslovakia had with France proved useless. This was also reflected by the fact that especially the French government had expressed the view that Czechoslovakia would be considered as being responsible for any resulting European war should the Czechoslovak Republic defend herself with force against German incursions.[52]
The slogan "About us, without us!" (O nás bez nás!; O nás bez nás!) summarizes the feelings of the people of Czechoslovakia (now Slovakia and the Czech Republic) towards the agreement.[53] With Sudetenland gone to Germany, Czecho-Slovakia (as the state was now renamed) lost its defensible border with Germany and the Czechoslovak border fortifications. Without them its independence became more nominal than real. Czechoslovakia also lost 70 per cent of its iron/steel industry, 70 per cent of its electrical power and 3.5 million citizens to Germany as a result of the settlement. The Sudeten Germans celebrated what they saw as their liberation. The imminent war, it seemed, had been avoided.[54]
The Nobel laureate, Thomas Mann, took to pen and pulpit in defense of his surrogate homeland proclaiming his pride at being a Czechoslovak citizen and praising the republic's achievements. He attacked a "Europe ready for slavery" writing that "The Czechoslovak people is ready to take up a fight for liberty and transcends its own fate" and "It is too late for the British government to save the peace. They have lost too many opportunities." President Beneš of Czechoslovakia was nominated for a Nobel Peace Prize in 1939.[55]
Germany
[edit]Though the British and French were pleased, a British diplomat in Berlin claimed he had been informed by a member of Hitler's entourage that soon after the meeting with Chamberlain Hitler had furiously said: "Gentlemen, this has been my first international conference and I can assure you that it will be my last."[56] On another occasion, he had been heard saying of Chamberlain: "If ever that silly old man comes interfering here again with his umbrella, I'll kick him downstairs and jump on his stomach in front of the photographers."[56][57][58] In one of his public speeches after Munich, Hitler declared: "Thank God we have no umbrella politicians in this country."[56][57][59]
Hitler felt cheated of the limited war against the Czechs which he had been aiming for all summer.[60] In early October, Chamberlain's press secretary asked for a public declaration of German friendship with Britain to strengthen Chamberlain's domestic position; Hitler instead delivered speeches denouncing Chamberlain's "governessy interference."[61] In August 1939, shortly before the invasion of Poland, Hitler told his generals: "Our enemies are men below average, not men of action, not masters. They are little worms. I saw them at Munich."[62]
Before the Munich Agreement, Hitler's determination to invade Czechoslovakia on 1 October 1938 had provoked a major crisis in the German command structure. The Chief of the General Staff, General Ludwig Beck, protested in a lengthy series of memos that it would start a world war that Germany would lose, and urged Hitler to put off the projected conflict. Hitler called Beck's arguments against war "kindische Kräfteberechnungen" ("childish force calculations"). On 4 August 1938, a secret Army meeting was held. Beck read his lengthy report to the assembled officers. They all agreed something had to be done to prevent certain disaster. Beck hoped they would all resign together but no one resigned except Beck. His replacement, General Franz Halder, sympathized with Beck and they both conspired with several top generals, Admiral Wilhelm Canaris (Chief of German Intelligence) and Graf von Helldorf (Berlin's Police Chief) to arrest Hitler the moment he gave the invasion order. This plan would only work if Britain issued a strong warning and a letter to the effect that they would fight to preserve Czechoslovakia. This would help to convince the German people that certain defeat awaited Germany. Agents were therefore sent to England to tell Chamberlain that an attack on Czechoslovakia was planned, and of their intention to overthrow Hitler if this occurred. The proposal was rejected by the British Cabinet and no such letter was issued. Accordingly, the proposed removal of Hitler did not go ahead.[63] On this basis it has been argued that the Munich Agreement kept Hitler in power—Halder remained bitter about Chamberlain's refusal for decades after the war—although whether the attempted removal would have been any more successful than the 1944 plot is doubtful.[64][34]
Britain and France
[edit]
The agreement was generally applauded. Prime Minister Daladier of France did not believe, as one scholar put it, that a European War was justified "to maintain three million Germans under Czech sovereignty." Gallup Polls in Britain, France, and the United States indicated that the majority of people supported the agreement. President Beneš of Czechoslovakia was nominated for a Nobel Peace Prize in 1939.[55]
The New York Times headline on the Munich agreement read "Hitler gets less than his Sudeten demands" and reported that a "joyful crowd" hailed Daladier on his return to France and that Chamberlain was "wildly cheered" on his return to Britain.[65]
In France, the only political party to oppose the Munich Agreement was the Communist Party.[66]
The British population had expected an imminent war, and the "statesman-like gesture" of Chamberlain was at first greeted with acclaim. He was greeted as a hero by the royal family and invited on the balcony at Buckingham Palace before he had presented the agreement to the British Parliament. The generally positive reaction quickly soured, despite royal patronage. However, there was opposition from the start. Clement Attlee and the Labour Party opposed the agreement, in alliance with two Conservative MPs, Duff Cooper and Vyvyan Adams, who had been seen up to then as a reactionary element in the Conservative Party.[67]
Daladier believed that Hitler's ultimate goals were a threat. He told the British in a late April 1938 meeting that Hitler's real long-term aim was to secure "a domination of the Continent in comparison with which the ambitions of Napoleon were feeble." He went on to say: "Today it is the turn of Czechoslovakia. Tomorrow it will be the turn of Poland and Romania. When Germany has obtained the oil and wheat it needs, she will turn on the West. Certainly we must multiply our efforts to avoid war. But that will not be obtained unless Great Britain and France stick together, intervening in Prague for new concessions but declaring at the same time that they will safeguard the independence of Czechoslovakia. If, on the contrary, the Western Powers capitulate again they will only precipitate the war they wish to avoid."[68] Perhaps discouraged by the arguments of French military leaders and civilian officials regarding their unprepared military and weak financial situation, and still traumatized by France's bloodbath in World War I, which he had personally witnessed, Daladier ultimately let Chamberlain have his way. On his return to Paris, Daladier, who had expected a hostile crowd, was acclaimed.[50]
In the days following Munich, Chamberlain received more than 20,000 letters and telegrams of thanks, and gifts including 6000 assorted bulbs from grateful Dutch admirers and a cross from Pope Pius XI.[69]
Poland
[edit]
Poland was building up a secret Polish organization in the area of Trans-Olza from 1935.[70] In summer 1938, Poland tried to organize guerrilla groups in the area.[70] On 21 September, Poland officially requested a direct transfer of the area to its own control. Polish envoy to Prague Kazimierz Papée marked that the return of Cieszyn Silesia will be a sign of a goodwill and the "redress of injustice" of 1920.[71] Similar notes were sent to Paris and London with a request that Polish minority in Czechoslovakia should gain the same rights as Sudeten Germans.[72] On the next day Beneš send a letter to Polish president Ignacy Mościcki with a promise of "border's rectification", but the letter was delivered only on 26 September.[73] The answer of Mościcki delivered on 27 September was evasive, but it was accompanied with the demand of Polish government to hand over two Trans-Olza counties immediately, as a prelude to ultimate settlement of the border dispute.[74] Beneš's answer wasn't conclusive: he agreed to hand over the disputed territory to Poland but argued that it could not be done on the eve of the German invasion, because it would disrupt Czechoslovak preparations for war. Poles recognised the answer as playing for time.[73]
Polish diplomatic actions were accompanied by placing army along the Czechoslovak border on 23–24 September and by giving an order to the so-called "battle units" of Trans-Olza Poles and the "Trans-Olza Legion", a paramilitary organisation that was made up of volunteers from all over Poland, to cross the border to Czechoslovakia and attack Czechoslovak units.[70] The few who crossed, however, were repulsed by Czechoslovak forces and retreated to Poland.[70]
The Polish ambassador in Germany learned about the results of Munich Conference on 30 September from Ribbentrop, who assured him that Berlin conditioned the guarantees for the remainder of Czechoslovakia on the fulfilment of Polish and Hungarian territorial demands.[75] Polish foreign minister Józef Beck was disappointed with such a turn of events. In his own words the conference was "an attempt by the directorate of great powers to impose binding decisions on other states (and Poland cannot agree on that, as it would then be reduced to a political object that others conduct at their will)."[76] As a result, at 11:45 p.m. on 30 September, 11 hours after the Czechoslovak government accepted the Munich terms, Poland gave an ultimatum to the Czechoslovak government.[77] It demanded the immediate evacuation of Czechoslovak troops and police and gave Prague time until noon the following day. At 11:45 a.m. on 1 October the Czechoslovak Foreign Ministry called the Polish ambassador in Prague and told him that Poland could have what it wanted but then requested a 24 hour delay. On 2 October, the Polish Army, commanded by General Władysław Bortnowski, annexed an area of 801.5 km2 with a population of 227,399 people. Administratively the annexed area was divided between Frysztat County and Cieszyn County.[78] The historian Dariusz Baliszewski wrote that during the annexation there was no co-operation between Polish and German troops, but there were cases of co-operation between Polish and Czech troops defending territory against Germans, for example in Bohumín.[79]
The Polish ultimatum finally led Beneš to decide, by his own account, to abandon any idea of resisting the settlement (Czechoslovakia would have been attacked on all sides).[80]
The Germans were delighted with that outcome and were happy to give up the sacrifice of a small provincial rail centre to Poland in exchange for the ensuing propaganda benefits. It spread the blame of the partition of Czechoslovakia, made Poland a participant in the process and confused political expectations. Poland was accused of being an accomplice of Germany.[81] However, there was no formal agreement between Poland and Germany about Czechoslovakia at any time.[82]
The Chief of the General Staff of the Czechoslovak Army, General Ludvík Krejčí, reported on 29 September that "Our army will in about two days' time be in full condition to withstand an attack even by all Germany's forces together, provided Poland does not move against us."[83]
Historians such as H.L. Roberts[84] and Anna Cienciala[85] have characterised Beck's actions during the crisis as unfriendly to Czechoslovakia, but not actively seeking its destruction. Whilst Stalin-era Polish historiography typically followed the line that Beck had been a "German Agent" and had collaborated with Germany, post-1956 historiography has generally rejected this characterisation.[86]
Hungary
[edit]Hungary followed Polish request for transfer of territory with its own request on 22 September.[71] Hungarian demands were ultimately fulfilled during the Vienna Arbitration on 2 November 1938.
Soviet Union
[edit]
Joseph Stalin was upset by the results of the Munich conference. On 2 May 1935, France and the Soviet Union signed the Franco-Soviet Treaty of Mutual Assistance with the aim of containing Nazi Germany's aggression.[87] The Soviets, who had a mutual military assistance treaty with Czechoslovakia, felt betrayed by France, which also had a mutual military assistance treaty with Czechoslovakia.[88] The British and French mostly used the Soviets as a threat to dangle over the Germans. Stalin concluded that the West had colluded with Hitler to hand over a country in Central Europe to the Germans, causing concern that they might do the same to the Soviet Union in the future to allow its partition between the western nations. This belief led the Soviet Union to reorient its foreign policy towards a rapprochement with Germany, which eventually led to the signing of the Molotov–Ribbentrop Pact in 1939.[89]
In 1938, the Soviet Union was allied with France and Czechoslovakia. By September 1939, the Soviets were to all intents and purposes a co-belligerent with Nazi Germany, due to Stalin's fears of a second Munich Agreement with the Soviet Union replacing Czechoslovakia. Thus, the agreement indirectly contributed to the outbreak of war in 1939.[90]
Elsewhere
[edit]The Australian Prime Minister Joseph Lyons said, "We owe heartfelt thanks to all responsible for the outcome, and appreciate very much the efforts of President Roosevelt and Signor Mussolini to bring about the Munich conference of the Powers at which a united desire for peace has been shown."[91]
Later opinions
[edit]As the threats of Germany and of a European war became more evident, opinions on the agreement became more hostile. Chamberlain was excoriated for his role as one of the "Men of Munich", in books such as the 1940 Guilty Men. A rare wartime defence of the agreement came in 1944 from Viscount Maugham, who had been Lord Chancellor. Maugham viewed the decision to establish a Czechoslovak state including substantial German and Hungarian minorities as a "dangerous experiment" in the light of previous disputes and ascribed the agreement as caused largely by France's need to extricate itself from its treaty obligations in the light of its unpreparedness for war.[92] After the war, Churchill's history of the period, The Gathering Storm (1948), asserted that Chamberlain's appeasement of Hitler at Munich had been wrong and recorded Churchill's prewar warnings of Hitler's plan of aggression and the folly of Britain's persisting with disarmament after Germany had achieved air parity with Britain. Although Churchill recognized that Chamberlain acted from noble motives, he argued that Hitler should have been resisted over Czechoslovakia and that efforts should have been made to involve the Soviet Union.[93]
In his postwar memoirs, Churchill, an opponent of appeasement, lumped Poland and Hungary, both of which subsequently annexed parts of Czechoslovakia containing Poles and Hungarians, with Germany as "vultures upon the carcass of Czechoslovakia."[94]
The American historian William L. Shirer, in his The Rise and Fall of the Third Reich (1960), took the view that although Hitler was not bluffing about his intention to invade, Czechoslovakia could have offered significant resistance. Shirer believed that Britain and France had enough air defences to avoid serious bombing of London and Paris and could have pursued a rapid and successful war against Germany.[95] He quotes Churchill as saying the agreement meant that "Britain and France were in a much worse position compared to Hitler's Germany."[54] After Hitler personally inspected the Czech fortifications, he privately said to Joseph Goebbels that "we would have shed a lot of blood" and that it was fortunate that there had been no fighting.[96]
Consequences
[edit]
On 5 October, Beneš resigned as President of Czechoslovakia since he realized that the fall of Czechoslovakia was inevitable. After the outbreak of World War II, he formed a Czechoslovak government-in-exile in London. On 6 December 1938, the French-German Non-aggression Pact was signed in Paris by French Foreign Minister Bonnet and German Foreign Minister Joachim von Ribbentrop.[97][98][99]
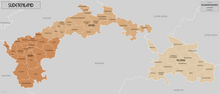
Nazi Germany occupied the Sudetenland from 1938 to 1945.[100]
First Vienna Award to Hungary
[edit]


In early November 1938, under the First Vienna Award, after the failed negotiations between Czechoslovakia and Hungary, as a recommendation to settle the territorial disputes by the appendix of the Munich Agreement, the German-Italian arbitration required Czechoslovakia to cede southern Slovakia to Hungary, and Poland independently gained small territorial cessions shortly afterward (Trans-Olza).[101]
Bohemia, Moravia and Silesia lost about 38% of their combined area to Germany, with some 2.8 million German and 513,000 to 750,000[102][103] Czech inhabitants. Hungary, in turn, received 11,882 km2 (4,588 sq mi) in southern Slovakia and southern Carpathian Ruthenia. According to a 1941 census, about 86.5% of the population in the territory was Hungarian. Slovakia lost 10,390 km2 (4,010 sq mi) and 854,218 inhabitants for Hungary (according to a Czechoslovak 1930 census about 59% were Hungarians and 32% were Slovaks and Czechs[104]). Poland annexed the town of Český Těšín with the surrounding area (some 906 km2 (350 sq mi), with 250,000 inhabitants. Poles made up about 36% of the population, down from 69% in 1910[105])[106] and two minor border areas in northern Slovakia, more precisely in the regions Spiš and Orava. (226 km2 (87 sq mi), 4,280 inhabitants, only 0.3% Poles).
Soon after Munich, 115,000 Czechs and 30,000 Germans fled to the rump of Czechoslovakia. According to the Institute for Refugee Assistance, the actual count of refugees on 1 March 1939 stood at almost 150,000.[107]
On 4 December 1938, elections in Reichsgau Sudetenland had 97.3% of the adult population vote for the Nazi Party. About half-a-million Sudeten Germans joined the Nazi Party, 17.3% of the German population in Sudetenland (the average NSDAP participation in Nazi Germany was 7.9%). Thus, the Sudetenland was the most "pro-Nazi" region in Nazi Germany.[108]
Because of their knowledge of Czech, many Sudeten Germans were employed in the administration of the Protectorate of Bohemia and Moravia as well as in Nazi organisations, such as the Gestapo. The most notable of them was Karl Hermann Frank, SS and Police General and Secretary of State in the Protectorate.[109]
German invasion of rump Czechoslovakia
[edit]In 1937, the Wehrmacht had formulated a plan, "Operation Green" (Fall Grün) for the invasion of Czechoslovakia. It was implemented shortly after the proclamation of the Slovak State on 15 March 1939.[110] On 14 March, Slovakia seceded from Czechoslovakia and became a separate Nazi-subordinate state. The following day, Carpatho-Ukraine proclaimed independence as well, but after three days, it was completely occupied and annexed by Hungary. Czechoslovak President Emil Hácha traveled to Berlin and was left waiting, and orders to invade had already been given. During the meeting with Hitler, Hácha was threatened with the bombing of Prague if he refused to order the Czech troops to lay down their arms. That news induced a heart attack from which he was revived by an injection from Hitler's doctor. Hácha then agreed to sign the communiqué accepting the German occupation of the remainder of Bohemia and Moravia, "which in its unctuous mendacity was remarkable even for the Nazis."[111] Churchill's prediction was fulfilled, as German armies entered Prague and proceeded to occupy the rest of the country, which was transformed into a protectorate of the Reich. In March 1939, Konstantin von Neurath was appointed as Reichsprotektor and served as Hitler's personal representative in the protectorate. Immediately after the occupation, a wave of arrests began, mostly of refugees from Germany, Jews and Czech public figures. By November, Jewish children had been expelled from their schools and their parents fired from their jobs. Universities and colleges were closed after demonstrations against the occupation of Czechoslovakia. Over 1200 students were sent to concentration camps, and nine student leaders were executed on 17 November (International Students' Day).[112]
By seizing Bohemia and Moravia, Nazi Germany gained all of the skilled labour force and heavy industry located there as well as all the weapons of the Czechoslovak Army. During the 1940 Battle of France, roughly 25% of all German weapons came from the protectorate. Nazi Germany also gained all of the Czechoslovakia's gold treasure, including gold stored in the Bank of England. Of a total 227 tons of gold found after the war in salt mines, only 18.4 tons were returned to Czechoslovakia in 1982, but most of it came from Czechoslovakia. Czechoslovakia was also forced to "sell" war material to the Wehrmacht for 648 million of prewar Czechoslovak koruna, a debt that was never repaid.[113]

Chamberlain claimed the Prague annexation was a "completely different category" that moved beyond the legitimate Versailles grievances.[114] Meanwhile, concerns arose in Britain that Poland, which was now encircled by many German possessions, would become the next target of Nazi expansionism. That was made apparent by the dispute over the Polish Corridor and the Free City of Danzig and resulted in the signing of an Anglo-Polish military alliance. That made the Polish government refuse to accept German negotiation proposals over the Polish Corridor and the status of Danzig.[115] Chamberlain felt betrayed by the Nazi seizure of Czechoslovakia, realized that his policy of appeasement towards Hitler had failed and so began to take a much harder line against Germany. He immediately began to mobilize the British armed forces to a war footing, and France did the same. Italy saw itself threatened by the British and French fleets and started its own invasion of Albania in April 1939.[116]
Strengthening of Wehrmacht armaments
[edit]Since most of the border defences had been in the territory ceded as a consequence of the Munich Agreement, the rest of Czechoslovakia was entirely open to further invasion despite its relatively-large stockpiles of modern armaments. In a speech delivered in the Reichstag, Hitler expressed the importance of the occupation for strengthening of German military and noted that by occupying Czechoslovakia, Germany gained 2,175 field guns and cannons, 469 tanks, 500 anti-aircraft artillery pieces, 43,000 machine guns, 1,090,000 military rifles, 114,000 pistols, about a billion rounds of small-arms ammunition, and 3 million rounds of anti-aircraft ammunition. That could then arm about half of the Wehrmacht.[117] Czechoslovak weapons later played a major role in the German conquest of Poland and France, the latter having urged Czechoslovakia into surrendering the Sudetenland in 1938.[full citation needed]
Birth of German resistance in military
[edit]In Germany, the Sudeten crisis led to the so-called Oster conspiracy. General Hans Oster, the deputy head of the Abwehr, and prominent figures within the German military opposed the regime for its behaviour, which threatened to bring Germany into a war that they believed it was not ready to fight. They discussed overthrowing Hitler and the regime through a planned storming of the Reich Chancellery by forces loyal to the plot.[118]
Italian colonial demands from France
[edit]Italy strongly supported Germany at Munich, and a few weeks later, in October 1938, tried to use its advantage to make new demands on France. Mussolini demanded a free port at Djibouti, control of the Addis Ababa-Djibouti railroad, Italian participation in the management of Suez Canal Company, some form of French-Italian condominium over Tunisia and the preservation of Italian culture in French-held Corsica with no French assimilation of the people. France rejected those demands and began threatening naval maneuvers as a warning to Italy.[119]
Quotations from key participants
[edit]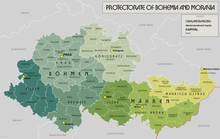
Germany stated that the incorporation of Austria into the Reich resulted in borders with Czechoslovakia that were a great danger to German security, and that this allowed Germany to be encircled by the Western Powers.[120]
Neville Chamberlain announced the deal at Heston Aerodrome as follows:
... the settlement of the Czechoslovak problem, which has now been achieved is, in my view, only the prelude to a larger settlement in which all Europe may find peace. This morning I had another talk with the German Chancellor, Herr Hitler, and here is the paper which bears his name upon it as well as mine. Some of you, perhaps, have already heard what it contains but I would just like to read it to you: ' ... We regard the agreement signed last night and the Anglo-German Naval Agreement as symbolic of the desire of our two peoples never to go to war with one another again.'[121]
Later that day he stood outside 10 Downing Street and again read from the document and concluded:
My good friends, for the second time in our history a British Prime Minister has returned from Germany bringing peace with honour. I believe it is peace for our time." (Chamberlain's reference to Disraeli's return from the Congress of Berlin in 1878)[121][122]
Winston Churchill, denouncing the Agreement in the House of Commons on 5 October 1938,[123] declared:
We have suffered a total and unmitigated defeat... you will find that in a period of time which may be measured by years, but may be measured by months, Czechoslovakia will be engulfed in the Nazi régime. We are in the presence of a disaster of the first magnitude... we have sustained a defeat without a war, the consequences of which will travel far with us along our road... we have passed an awful milestone in our history, when the whole equilibrium of Europe has been deranged, and that the terrible words have for the time being been pronounced against the Western democracies: "Thou art weighed in the balance and found wanting." And do not suppose that this is the end. This is only the beginning of the reckoning. This is only the first sip, the first foretaste of a bitter cup which will be proffered to us year by year unless by a supreme recovery of moral health and martial vigour, we arise again and take our stand for freedom as in the olden time.
On 13 August 1938, prior to the conference, Churchill had written in a letter to David Lloyd George:[124]
England has been offered a choice between war and shame. She has chosen shame, and will get war.
Legal nullification
[edit]During the Second World War, British Prime Minister Churchill, who opposed the agreement when it was signed, became determined that the terms of the agreement would not be upheld after the war and that the Sudeten territories should be returned to postwar Czechoslovakia. On 5 August 1942, Foreign Minister Anthony Eden sent the following note to Jan Masaryk:
In the light of recent exchanges of view between our Governments, I think it may be useful for me to make the following statement about the attitude of His Majesty's Government in the United Kingdom as regards Czecho-Slovakia.
In my letter of the 18th July, 1941, I informed your Excellency that the King had decided to accredit an Envoy Extraordinary and Minister Plenipotentiary to Dr. Beneš as President of the Czecho-Slovak Republic. I explained that this decision implied that His Majesty's Government in the United Kingdom regarded the juridical position of the President and Government of the Czecho-Slovak Republic as identical with that of the other Allied heads of States and Governments established in this country. The status of His Majesty's representative has recently been raised to that of an Ambassador.
The Prime Minister had already stated in a message broadcast to the Czecho-Slovak people on the 30th September, 1940, the attitude of His Majesty's Government in regard to the arrangements reached at Munich in 1938. Mr. Churchill then said that the Munich Agreement had been destroyed by the Germans. This statement was formally communicated to Dr. Beneš on the 11th November, 1940.
The foregoing statement and formal act of recognition have guided the policy of His Majesty's Government in regard to Czecho-Slovakia, but in order to avoid any possible misunderstanding, I desire to declare on behalf of His Majesty's Government in the United Kingdom that as Germany has deliberately destroyed the arrangements concerning Czecho-Slovakia reached in 1938, in which His Majesty's Government in the United Kingdom participated, His Majesty's Government regard themselves as free from any engagements in this respect. At the final settlement of the Czecho-Slovak frontiers to be reached at the end of the war they will not be influenced by any changes effected in and since 1938.
To which Masaryk replied as follows:
I have the honour to acknowledge the receipt of your note of the 5th August, 1942, and I avail myself of this opportunity to convey to your Excellency, on behalf of the Czecho-Slovak Government and of myself, as well as in the name of the whole Czecho-Slovak people who are at present suffering so terribly under the Nazi yoke, the expression of our warmest thanks.
Your Excellency's note emphasizes the fact that the formal act of recognition has guided the policy of His Majesty's Government in regard to Czecho-Slovakia, but, in order to avoid any possible misunderstanding, His Majesty's Government now desire to declare that, as Germany has deliberately destroyed the arrangements concerning Czecho-Slovakia reached in 1938, in which His Majesty's Government in the United Kingdom participated, His Majesty's Government regard themselves as free from any engagements in this respect. At the final settlement of the Czecho-Slovak frontiers to be reached at the end of the war, they will not be influenced by any changes effected in and since 1938.
My Government accept your Excellency's note as a practical solution of the questions and difficulties of vital importance for Czecho-Slovakia which emerged between our two countries as the consequence of the Munich Agreement, maintaining, of course, our political and juridical position with regard to the Munich Agreement and the events which followed it as expressed in the note of the Czecho-Slovak Ministry for Foreign Affairs of the 16th December, 1941. We consider your important note of the 5th August, 1942, as a highly significant act of justice towards Czecho-Slovakia, and we assure you of our real satisfaction and of our profound gratitude to your great country and nation. Between our two countries the Munich Agreement can now be considered as dead.[125]
In September 1942 the French National Committee, headed by Charles de Gaulle, proclaimed the Munich Agreement to be null and void from the very beginning, and on 17 August 1944, the French government reaffirmed this.[126] After Mussolini's fascist leadership had been replaced, the Italian Government followed suit and did the same.[126]
Following Allied victory and the defeat of Nazi Germany in 1945, the Sudetenland was returned to Czechoslovakia, while the German speaking majority was expelled in accordance with the international Potsdam Agreement.
"Ghost of Munich"
[edit]In the United States and the United Kingdom, the words "Munich" and "appeasement" are frequently invoked when demanding forthright, often military, action to resolve an international crisis and characterising a political opponent who condemns negotiation as weakness.[127] In 1950, US President Harry Truman invoked "Munich" to justify his military action in the Korean War: "The world learned from Munich that security cannot be bought by appeasement."[128] Many later crises were accompanied by cries of "Munich" from politicians and the media. In 1960, the conservative US Senator Barry Goldwater used "Munich" to describe a domestic political issue by saying that an attempt by the Republican Party to appeal to liberals was "the Munich of the Republican Party."[129] In 1962, General Curtis LeMay told US President John F. Kennedy that his refusal to bomb Cuba during the Cuban Missile Crisis was "almost as bad as the appeasement at Munich", a pointed barb given that his father Joseph P. Kennedy Sr. had supported appeasement in general in his capacity as Ambassador to Britain.[130][131] In 1965, US President Lyndon Johnson, in justifying increased military action in Vietnam, stated, "We learned from Hitler and Munich that success only feeds the appetite for aggression."[132]
Citing Munich in debates on foreign policy has continued to be common in the 21st century.[133] During negotiations for the Iran nuclear agreement mediated by Secretary of State John Kerry, Representative John Culberson, a Texas Republican Representative, tweeted the message "Worse than Munich." Kerry had himself invoked Munich in a speech in France advocating military action in Syria by saying, "This is our Munich moment."[134]
"Munich and appeasement", in the words of scholars Fredrik Logevall and Kenneth Osgood, "have become among the dirtiest words in American politics, synonymous with naivete and weakness, and signifying a craven willingness to barter away the nation's vital interests for empty promises." They claimed that the success of US foreign policy often depends upon a president withstanding "the inevitable charges of appeasement that accompany any decision to negotiate with hostile powers." The presidents who challenged the "tyranny of Munich" have often achieved policy breakthroughs and those who had cited Munich as a principle of US foreign policy had often led the nation into its "most enduring tragedies."[132]
The West German policy of staying neutral in the Arab–Israeli conflict after the Munich massacre and the following hijack of the Lufthansa Flight 615 in 1972, rather than taking a pro-Israel position, led to Israeli comparisons with the Munich Agreement of appeasement.[135]
See also
[edit]- Causes of World War II
- Lesson of Munich
- European foreign policy of the Chamberlain ministry
- Treaty of Prague (1973)
- Expulsion of Germans from Czechoslovakia
References
[edit]Notes
[edit]Citations
[edit]- ^ see the text at "Munich Pact September 30, 1938"
- ^ Text in League of Nations Treaty Series, 1924 "vol. 23", pp. 164–169.
- ^ a b Goldstein, Erik; Lukes, Igor (1999), The Munich Crisis, 1938: Prelude to World War II, New York, pp. 59–60, ISBN 9781136328398, retrieved 25 August 2019
{{citation}}: CS1 maint: location missing publisher (link) - ^ Ragsdale, Hugh (2001). "The Butenko Affair: Documents from Soviet-Romanian Relations in the Time of the Purges, Anschluss, and Munich". The Slavonic and East European Review. 79 (4): 698–720. doi:10.1353/see.2001.0004. ISSN 0037-6795. JSTOR 4213322.
- ^ Jesenský 2014, pp. 88–89.
- ^ office, Kafkadesk Prague (14 March 2021). "On this Day, in 1939: Slovakia declared its independence to side with Nazi Germany – Kafkadesk". kafkadesk.org. Retrieved 4 October 2021.
- ^ "Hoedl-Memoiren". joern.de. Retrieved 20 July 2019.
- ^ "What the British and the French Actually Thought About the Decision to Appease Hitler at Munich in 1938". TIME. 24 September 2019. Retrieved 29 April 2024.
- ^ "What's the context? 30 September 1938: The Munich Agreement – History of government". history.blog.gov.uk. 30 September 2013. Retrieved 29 April 2024.
- ^ "Munich Agreement", Encyclopædia Britannica. Retrieved 6 August 2018.
- ^ Statistický lexikon obcí v Republice československé I. Země česká. Prague. 1934.
{{cite book}}: CS1 maint: location missing publisher (link)
Statistický lexikon obcí v Republice česko7slovenské II. Země moravskoslezská. Prague. 1935.{{cite book}}: CS1 maint: location missing publisher (link) - ^ Glassheim, Eagle (2016). Cleansing the Czechoslovak borderlands: migration, environment, and health in the former Sudetenland. Pitt series in Russian and East European studies. Pittsburgh, Pa: University of Pittsburgh Press. ISBN 978-0-8229-6426-1. OCLC 951158062.
- ^ Douglas, R. M. (2012), Orderly and Humane, New Haven: Yale University Press, p. 9
- ^ Douglas, pp. 7–12
- ^ a b c d e f Eleanor L. Turk. The History of Germany. Westport, Connecticut: Greenwood Press, 1999. ISBN 9780313302749. p. 123.
- ^ Douglas, pp. 12–13
- ^ Noakes & Pridham 2010, pp. 100–101, Vol. 3.
- ^ Hruška, E. (2013). Boj o pohraničí: Sudetoněmecký Freikorps v roce 1938 (in Czech). Prague: Nakladatelství epocha. p. 11.
- ^ Douglas, p. 18
- ^ Noakes & Pridham 2010, p. 102, Vol. 3.
- ^ Noakes & Pridham 2010, vol. 3 p. 101.
- ^ Noakes & Pridham 2010, vol. 3 pp. 1001–1002.
- ^ a b Noakes & Pridham 2010, vol. 3 p. 102.
- ^ a b c Noakes & Pridham 2010, vol. 3 p. 104.
- ^ Hehn, Paul N (2005). A Low, Dishonest Decade: The Great Powers, Eastern Europe and the Economic Origins of World War II, 1930–1941. Bloomsbury Academic. p. 89. ISBN 9780826417619.
- ^ Noakes & Pridham 2010, vol. 3 pp. 102–103.
- ^ a b c d e Bell 1986, p. 238.
- ^ Noakes & Pridham 2010, vol. 2 p. 201.
- ^ a b c Noakes & Pridham 2010, vol. 3 p. 105.
- ^ Noakes & Pridham 2010, p. 105, Vol. 3.
- ^ a b c d e Adolf Hitler, Max Domarus. The Essential Hitler: Speeches and Commentary. Bolchazy-Carducci Publishers, 2007. ISBN 9780865166271. p. 626.
- ^ a b Adolf Hitler, Max Domarus. The Essential Hitler: Speeches and Commentary. Bolchazy-Carducci Publishers, 2007. ISBN 9780865166271. p. 627.
- ^ a b Bell 1986, p. 239.
- ^ a b c d e f g h i Reynolds, David (2009). Summits : six meetings that shaped the twentieth century. New York: Basic Books. ISBN 9780786744589. OCLC 646810103.
- ^ a b c d e f Santi Corvaja, Robert L. Miller. Hitler & Mussolini: The Secret Meetings. New York: Enigma Books, 2008. ISBN 9781929631421. p. 71.
- ^ Santi Corvaja, Robert L. Miller. Hitler & Mussolini: The Secret Meetings. New York: Enigma Books, 2008. ISBN 9781929631421. pp. 71–72.
- ^ a b c d e f g h i j k l m n Santi Corvaja, Robert L. Miller. Hitler & Mussolini: The Secret Meetings. New York: Enigma Books, 2008. ISBN 9781929631421. p. 72.
- ^ President Beneš' declaration made on 16 December 1941
- ^ Note of the Czechoslovak government-in-exile dated 22 February 1944
- ^ Constitutional Court of the Czech Republic (1997), Ruling No. II. ÚS 307/97 (in Czech), Brno
{{citation}}: CS1 maint: location missing publisher (link) Stran interpretace "kdy země vede válku", obsažené v čl. I Úmluvy o naturalizaci mezi Československem a Spojenými státy, publikované pod č. 169/1929 Sb. za účelem zjištění, zda je splněna podmínka státního občanství dle restitučních předpisů, Ústavní soud vychází z již v roce 1933 vypracované definice agrese Společnosti národů, která byla převzata do londýnské Úmluvy o agresi (CONVENITION DE DEFINITION DE L'AGRESSION), uzavřené dne 4. 7. 1933 Československem, dle které není třeba válku vyhlašovat (čl. II bod 2) a dle které je třeba za útočníka považovat ten stát, který první poskytne podporu ozbrojeným tlupám, jež se utvoří na jeho území a jež vpadnou na území druhého státu (čl. II bod 5). V souladu s nótou londýnské vlády ze dne 22. 2. 1944, navazující na prohlášení prezidenta republiky ze dne 16. 12. 1941 dle § 64 odst. 1 bod 3 tehdejší Ústavy, a v souladu s citovaným čl. II bod 5 má Ústavní soud za to, že dnem, kdy nastal stav války, a to s Německem, je den 17. 9. 1938, neboť tento den na pokyn Hitlera došlo k utvoření "Sudetoněmeckého svobodného sboru" (Freikorps) z uprchnuvších vůdců Henleinovy strany a několik málo hodin poté už tito vpadli na československé území ozbrojeni německými zbraněmi. - ^ Nigel Jones. Countdown to Valkyrie: The July Plot to Assassinate Hitler. pp. 73–74.
- ^ a b c d e f g h i j Santi Corvaja, Robert L. Miller. Hitler & Mussolini: The Secret Meetings. New York: Enigma Books, 2008. ISBN 9781929631421. p. 73.
- ^ Haslam, Jonathan (1983). Soviet Foreign Policy, 1930–33. The Impact of the Depression. New York: St. Martin's Press.
- ^ Domarus, Max; Hitler, Adolf (1990). Hitler: speeches and proclamations, 1932–1945 : the chronicle of a dictatorship. p. 1393.
- ^ "Neville Chamberlin on 'Appeasement' (1939)". www.historyguide.org.
- ^ Santi Corvaja, Robert L. Miller. Hitler & Mussolini: The Secret Meetings. New York: Enigma Books, 2008. ISBN 9781929631421. pp. 73–74.
- ^ a b c Santi Corvaja, Robert L. Miller. Hitler & Mussolini: The Secret Meetings. New York: Enigma Books, 2008. ISBN 9781929631421. p. 74.
- ^ Dallek, Robert (1995). Franklin D. Roosevelt and American Foreign Policy, 1932–1945: With a New Afterword. Oxford University Press. p. 166. ISBN 9780199826667.
- ^ Gilbert & Gott 1999, p. 178.
- ^ a b Susan Bindoff Butterworth, "Daladier and the Munich crisis: A reappraisal." Journal of Contemporary History 9.3 (1974): 191–216.
- ^ "Peacetime". Encyclopedia Britannica.
- ^ Kuklik, Jan. The validity of the Munich agreement and the process of the repudiation during the second world war as seen from a Czechoslovak perspective. p. 346.
- ^ "Czech Republic: Past Imperfect – 64 Years Later, Munich 'Betrayal' Still Defines Thought (Part 5)". Radio Free Europe/Radio Liberty. 19 July 2002.
- ^ a b Shirer 1960.
- ^ a b Douglas, pp. 14–15
- ^ a b c Kirkpatrick 1959, p. 135.
- ^ a b Richard Overy, 'Germany, "Domestic Crisis" and War in 1939', Past & Present No. 116 (Aug., 1987), p. 163, n. 74.
- ^ Robert Rothschild, Peace For Our Time (Brassey's Defence Publishers, 1988), p. 279.
- ^ Roger Parkinson, Peace For Our Time: Munich to Dunkirk – The Inside Story (London: Hart-Davis, 1971), p. 78.
- ^ Ian Kershaw, Hitler, 1936–1945: Nemesis (London: Penguin, 2001), pp. 122–123.
- ^ Robert Self, Neville Chamberlain (London: Routledge, 2006), p. 344.
- ^ John W. Wheeler-Bennett, The Nemesis of Power: The German Army in Politics 1918–1945 (London: Macmillan, 1964), p. 447.
- ^ Parssinen 2004.
- ^ Leach, Barry (1989). Hitler's Generals. Quill. p. 105.
- ^ "Britain and Germany Make Anti-War Pact; Hitler Gets Less Than His Sudeten Demands; Polish Ultimatum Threatens Action Today". The New York Times. Retrieved 20 July 2019.
- ^ "En France, seuls les communistes, deux députés et quelques journalistes ont combattu l'accord". Le Monde.fr. 30 September 1968.
- ^ Adolf Sturmthal, " Labor's Road to Munich". in The Tragedy of European Labor 1918–1939 (1943) pp. 297–324.
- ^ Shirer 1969, pp. 339–340.
- ^ David Faber, Munich. The 1938 Appeasement Crisis (2008), p. 421
- ^ a b c d Goldstein & Lukes 1999, p. 122.
- ^ a b Jesenský 2014, p. 82.
- ^ Rak 2019, p. 405.
- ^ a b Kornat 2012, p. 157.
- ^ Majewski 2019, pp. 459–460.
- ^ Rak 2019, p. 409.
- ^ Rak 2019, p. 410.
- ^ Goldstein & Lukes 1999, p. 66.
- ^ "Dziennik Ustaw Śląskich, 31.10.1938, [R. 17], nr 18 – Silesian Digital Library". 4258 III. 14 February 2008. Retrieved 29 August 2019.
- ^ Baliszewski, Mariusz. "Prawda o Zaolziu – Uważam Rze Historia". historia.uwazamrze.pl (in Polish). Retrieved 12 October 2019.
- ^ Taylor, A.J.P. (1967). Origin of the Second World War. Penguns Books. p. 241.
- ^ Watt, Richard (1998). Bitter Glory. Poland and its fate 1918–1939. New York. Hippocrene Books. p. 511. ISBN 9780781806732.
- ^ Weinberg, Gerhard L. (1975). "German Foreign Policy and Poland, 1937–38". The Polish Review. 20 (1): 16. JSTOR 27920627. Retrieved 13 February 2021.
- ^ Stone, Norman (1989). Czechoslovakia Crossroads and Crises. Palgrave Macmillan UK. p. 119. ISBN 9781349106462.
- ^ Roberts, H.L. (1960). "The Diplomacy of Colonel Beck". In Craig, Gordon A.; Gilbert, Felix (eds.). The Diplomats 1919–1939. Princeton. pp. 603, 611.
Even Beck's unpleasant performance at the time of Munich was not planned in concert with the Germans... He did not like Czechoslovakia, but he did not plot its destruction
- ^ Cienciala, A.M. (30 November 1999). "The Munich crisis of 1938: Plans and strategy in Warsaw in the context of the western appeasement of Germany". In Goldstein, Erik; Lukes, Igor (eds.). The Munich Crisis, 1938 Prelude to World War II. Routledge. pp. 57–58. doi:10.4324/9780203045077. ISBN 9780203045077. Retrieved 13 February 2021.
- ^ Gromada, Thadeus V. (1981). "Joseph Beck in the Light of Recent Polish Historiography". The Polish Review. 26 (3): 68–71. JSTOR 25777835. Retrieved 13 February 2021.
- ^ Jabara Carley, Michael. "Who Betrayed Whom? Franco-Anglo-Soviet Relations, 1932–1939" (PDF). Université de Montréal.
- ^ "Franco-Czech Treaty". Time. 7 January 1924.
- ^ Hildebrand 1991.
- ^ Sakwa, Richard (1999). The Rise and Fall of the Soviet Union 1917–1991. Routledge. p. 225. ISBN 0415122899.
- ^ "Empire Comment on the Agreement". The Manchester Guardian. 1 October 1938. p. 7.
We owe heartfelt thanks to all responsible for the outcome, and appreciate very much the efforts of President Roosevelt and Signor Mussolini to bring about the Munich conference of the Powers at which a united desire for peace has been shown.
- ^ Maugham 1944.
- ^ Winston Churchill, The Gathering Storm (1948) p 318.
- ^ Churchill, Winston S (2002). The Second World War. Vol. 1: The Gathering Storm. RosettaBooks LLC. pp. 289–290. ISBN 9780795308321.
- ^ Shirer 1960, p. 520.
- ^ Joseph Goebbels diary, 2 October 1938, p. 2.
- ^ Gibler, Douglas M (2008). International Military Alliances, 1648–2008. CQ Press. p. 203. ISBN 9781604266849.
- ^ "The Franco-German Declaration of December 6th, 1938". Retrieved 11 June 2020.
- ^ France Signs "No-War" Pact with Germany, Chicago Tribune, 7 December 1938
- ^ Glassheim, Eagle (2006). "Ethnic Cleansing, Communism, and Environmental Devastation in Czechoslovakia's Borderlands, 1945–1989". The Journal of Modern History. 78 (1): 65–92. doi:10.1086/499795. S2CID 142647561.
- ^ Anthony Komjathy, "The First Vienna Award (November 2, 1938)." Austrian History Yearbook 15 (1979): 130–156.
- ^ "K otázce vysídlení občanů ČSR ze Sudet, Těšínska, Podkarpatské Rusi a Slovenské republiky v letech 1938/1939". Archived from the original on 2 December 2014. Retrieved 2 December 2014.
- ^ "Fakta o vyhnání Čechů ze Sudet". bohumildolezal.cz. Retrieved 20 July 2019.
- ^ Hetényi, Martin (2008). "Slovak-Hungarian border in the years 1938–1945" (PDF). Retrieved 17 July 2021.
- ^ Irena Bogoczová, Jana Raclavska. "Report about the national and language situation in the area around Czeski Cieszyn/Český Těšín in the Czech Republic." Czeski Cieszyn/Český Těšín Papers. Nr 7, EUR.AC research. November 2006. p. 2. (source: Zahradnik. "Struktura narodowościowa Zaolzia na podstawie spisów ludności 1880–1991." Třinec 1991).
- ^ Siwek n.d.
- ^ Forced displacement of Czech population under Nazis in 1938 and 1943, Radio Prague
- ^ Zimmerman 1999.
- ^ Valdis O. Lumans, "The Ethnic German Minority of Slovakia and the Third Reich, 1938–45." Central European History 15.3 (1982): 266–296.
- ^ Herzstein 1980, p. 184.
- ^ Noakes, J. and Pridham, G. (eds) (2010) [2001] "Nazism 1919–1945", Vol 3, Foreign Policy, War and Racial Extermination, University of Exeter Press, Exeter, p. 119
- ^ N.J.W. Goda, Tales from Spandau. Nazi Criminals and the Cold War (2007). pp. 161–163.
- ^ David Blaazer, "Finance and the end of appeasement: the Bank of England, the National Government and the Czech gold." Journal of Contemporary History 40.1 (2005): 25–39.
- ^ McDonough, 2002, p. 73
- ^ Władysław W. Kulski, "The Anglo-Polish Agreement of August 25, 1939", The Polish Review, (1976) 21 (1/2): 23–40.
- ^ Winston Churchill, The Gathering Storm (1948) pp 381–401.
- ^ Motl, Stanislav (2007). Kam zmizel zlatý poklad republiky (in Czech) (2nd ed.). Prague: Rybka publishers.
- ^ Terry M. Parssinen, The Oster Conspiracy of 1938: The Unknown Story of the Military Plot to Kill Hitler and Avert World War II (2001). [ISBN missing]
- ^ H. James Burgwyn, Italian Foreign Policy in the Interwar Period, 1918–1940 (Praeger Publishers, 1997), pp. 182–185. [ISBN missing]
- ^ Müller 1943, pp. 116–130.
- ^ a b The Oxford Dictionary of Quotations
- ^ "Neville Chamberlain". UK government. Archived from the original on 2 April 2012. Retrieved 23 September 2008.
- ^ "National Churchill Museum". Retrieved 1 October 2016.
- ^ "The Churchill Center". Archived from the original on 5 October 2016. Retrieved 1 October 2016.
- ^ League of Nations Treaty Series, pp. 378–380.
- ^ a b Jan, Kuklík (2015). Czech Law in Historical Contexts. Charles University in Prague, Karolinum Press. ISBN 9788024628608. Retrieved 20 July 2019 – via Google Books.
- ^ Yuen Foong Khong (1992). Analogies at War: Korea, Munich, Dien Bien Phu, and the Vietnam Decisions of 1965. Princeton UP. pp. 4–7. ISBN 0691025355.
- ^ "The Munich Analogy: The Korean War", Encyclopedia of the New American Nation. Retrieved 11 January 2018.
- ^ Dallek, Matthew (December 1995). "The Conservative 1960s". The Atlantic. p. 6. Retrieved 5 September 2020.
- ^ Dobbs, Michael (2008). One minute to midnight: Kennedy, Khrushchev, and Castro on the brink of nuclear war (1st ed.). New York: Alfred A. Knopf. ISBN 9780307269362. OCLC 608213334.
- ^ Wheatcroft, Geoffrey (3 December 2013), "On the Use and Abuse of Munich". Retrieved 11 January 2018
- ^ a b Logevall and Osgood (2010).
- ^ Jeffrey Record (2002), Making War, Thinking History: Munich, Vietnam, and Presidential Uses of Force from Korea to Kosovo
- ^ "Kerry: 'This is our Munich moment'". BBC News. Retrieved 4 October 2021.
- ^ "Deutsche Feigheit". Der Spiegel (in German). 11 November 1972. Archived from the original on 19 October 2013. Retrieved 16 July 2013.
Bibliography
[edit]Books
[edit]- Bell, P. M. H. (1986). The Second World War in Europe. Harlow, Essex: Longman.
- Douglas, R.M. (2012). Orderly and Humane: The Expulsion of the Germans after the Second World War. New Haven: Yale University Press.
- Faber, David (2008). Munich: The 1938 Appeasement Crisis. New York & London: Simon & Schuster. ISBN 978-1-84737-008-2.
- Gilbert, Martin; Gott, Richard (1999) [1967]. The Appeasers. London: Frank Cass & Co.
- Goldstein, Erik; Lukes, Igor (1967). The Munich Crisis, 1938: Prelude to World War II. London: Weidenfeld & Nicolson. ISBN 9781136328398.
- Herzstein, Robert Edwin (1980). The Nazis. World War II series. New York: Time-Life Books.
- Hildebrand, Klaus (1991). Das Dritte Reich (in German). München: Oldenbourg Grundriss der Geschichte.
- Jesenský, Marcel (2014). The Slovak–Polish Border, 1918–1947. Palgrave Macmillan. ISBN 9781137449641.
- Kirkpatrick, Ivone (1959). The Inner Circle. Macmillan.
- Kornat, Marek (2012). Polityka zagraniczna Polski 1938–1939. Cztery decyzje Józefa Becka (PDF) (in Polish). Wydawnictwo Oskar.
- Majewski, Piotr M. (2019). Kiedy wybuchnie wojna? 1938. Studium kryzysu [When will the war break out? 1938: A study of the crisis] (in Polish). Warsaw: Krytyka Polityczna. ISBN 9788366232419.
- Maugham, Viscount (1944). The Truth about the Munich Crisis. William Heinemann Ltd.
- McDonough, F. (2002). Hitler, Chamberlain and Appeasement. Cambridge: Cambridge University Press.
- Müller, Reinhard (1943). Deutschland (in German). München and Berlin: Sechster Teil, R. Oldenbourg Verlag.
- Noakes, J.; Pridham, G. (2010) [2001]. Nazism 1919–1945: Foreign Policy War, and Racial Extermination. Vol. II (2nd ed.). Devon: University of Exeter Press.
- Parssinen, Terry (2004). The Oster Conspiracy of 1938: The Unknown Story of the Military Plot to Kill Hitler. Pimlico Press. ISBN 1844133079.
- Rak, Krzysztof (2019). Polska – niespełniony sojusznik Hitlera (in Polish). Bellona.
- Shirer, William L. (1960). The Rise and Fall of the Third Reich. Pan.
- Shirer, William L. (1969). The Collapse of the Third Republic: An Inquiry into the Fall of France in 1940. Da Capo Press.
- Zimmerman, Volker (1999). Die Sudetendeutschen im NS-Staat. Politik und Stimmung der Bevölkerung im Reichsgau Sudetenland (1938–1945) (in German). Essen. ISBN 3884747703.
Websites
[edit]- Siwek, Tadeusz (n.d.). "Statystyczni i niestatystyczni Polacy w Republice Czeskiej" (in Polish). Wspólnota Polska.
- League of Nations Treaty Series (PDF). Vol. 204. 1941–1943.
Journal articles
[edit]- Fredrik Logevall; Kenneth Alan Osgood (July 2010). "The Ghost of Munich: America's Appeasement Complex". World Affairs. 173 (2): 13–26. ISSN 1940-1582. Wikidata Q125208142.
Further reading
[edit]- Bouverie, Tim (2019). Appeasing Hitler: Chamberlain, Churchill and the Road to War. London: The Bodley Head. ISBN 978-1847-924407.
- Butterworth, Susan Bindoff. "Daladier and the Munich crisis: A reappraisal." Journal of Contemporary History 9.3 (1974): 191–216
- Cole, Robert A. "Appeasing Hitler: The Munich Crisis of 1938: A Teaching and Learning Resource", New England Journal of History (2010) 66#2 pp 1–30.
- Duroselle, Jean-Baptiste. France and the Nazi Threat: The Collapse of French Diplomacy 1932–1939 (2004) pp 277–301.
- Dray, W. H. (1978). "Concepts of Causation in A. J. P. Taylor's Account of the Origins of the Second World War". History and Theory. 17 (2): 149–174. doi:10.2307/2504843. JSTOR 2504843.
- Farnham, Barbara Reardon. Roosevelt and the Munich crisis: A study of political decision-making (Princeton University Press, 2021).
- Goddard, Stacie E. "The rhetoric of appeasement: Hitler's legitimation and British foreign policy, 1938–39." Security Studies 24.1 (2015): 95–130.
- Gottlieb, Julie et al. eds. The Munich Crisis, politics and the people: International, transnational and comparative perspectives (2021) excerpt
- Jordan, Nicole. "Léon Blum and Czechoslovakia, 1936–1938." French History 5#1 (1991): 48–73.
- Lukes, Igor and Erik Goldstein, eds. The Munich crisis, 1938: prelude to World War II (1999); Essays by scholars. online
- Phillips, Adrian (2019). Fighting Churchill, Appeasing Hitler. New York and London: Pegasus. ISBN 978-1-64313-221-1.
- Record, Jeffrey. "The use and abuse of history: Munich, Vietnam and Iraq." Survival (2019) pp. 163–180.
- Riggs, Bruce Timothy. "Geoffrey Dawson, editor of "The Times" (London), and his contribution to the appeasement movement" (PhD dissertation, U of North Texas, 1993 online), bibliography pp 229–233.
- Ripsman, Norrin M. and Jack S. Levy. 2008. "Wishful Thinking or Buying Time? The Logic of British Appeasement in the 1930s." International Security 33(2): 148–181.
- Smetana, Vít. "Ten propositions about Munich 1938. On the fateful event of Czech and European history – without legends and national stereotypes." Czech Journal of Contemporary History 7.7 (2019): 5–14. online Archived 19 March 2022 at the Wayback Machine
- Thomas, Martin. "France and the Czechoslovak crisis." Diplomacy and Statecraft 10.23 (1999): 122–159.
- Watt, Donald Cameron. How war came: the immediate origins of the Second World War, 1938–1939 (1989) online free to borrow
- Werstein, Irving. Betrayal: the Munich pact of 1938 (1969) online free to borrow
- Wheeler-Bennett, John. Munich: Prologue to tragedy (1948).
External links
[edit]- The Munich Agreement – Text of the Munich Agreement on-line
- The Munich Agreement in contemporary radio news broadcasts Archived 24 May 2011 at the Wayback Machine – Actual radio news broadcasts documenting evolution of the crisis
- The Munich Agreement Original reports from The Times
- British Pathe newsreel (includes Chamberlain's speech at Heston aerodrome) Archived 8 July 2011 at the Wayback Machine (Adobe Flash)
- Peace: And the Crisis Begins Archived 15 July 2011 at the Wayback Machine from a broadcast by Dorothy Thompson, 1 October 1938
- Post-blogging the Sudeten Crisis – A day by day summary of the crisis
- Text of the 1942 exchange of notes nullifying the Munich agreement
- Photocopy of The Munich Agreement from Politisches Archiv des Auswärtigen Amts in Berlin (text in German) and from The National Archives in London (map).
- Map of Europe during Munich Agreement Archived 1 August 2014 at the Wayback Machine at omniatlas
- Dr. Quigley explains how Nazi Germany seized a stronger Czechoslovakia
- List of Czechoslovak villages ceded to Germany, Hungary and Poland, a book in Slovak. Územie a obyvatelstvo Slovenskej republiky a prehľad obcí a okresov odstúpenych Nemecku, Maďarsku a Poľsku. Bratislava: Štátny štatistický úrad, 1939. 92 p. – available online at ULB's Digital Library
- Munich Agreement
- 1938 conferences
- 1938 in France
- 1938 in Germany
- 1938 in Italy
- 1938 in the United Kingdom
- September 1938 events
- Partition (politics)
- Treaties concluded in 1938
- Treaties of Nazi Germany
- Treaties of the French Third Republic
- Treaties of the Kingdom of Italy (1861–1946)
- Treaties of the United Kingdom
- Territorial evolution of Hungary
- 1930s in Munich
